Teoremas de Thales

Cuando en geometría hablemos del Teorema de Tales (o Thales) , debemos aclarar a cuál nos referimos ya que existen dos teoremas atribuidos al matemático griego Tales de Mileto en el siglo VI a. C. Primer teorema Como definición previa al enunciado del teorema, es necesario establecer que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre si. El primer teorema de Tales recoge uno de los postulados más básicos de la geometría, a saber, que:Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes.
Entonces, veamos el primer Teorema de Tales en un triángulo :
Dado un triángulo ABC , si se traza un segmento paralelo, B'C', a uno de los lados del triángulo, se obtiene otro triángulo AB'C' , cuyos lados son proporcionales a los del triángulo ABC .


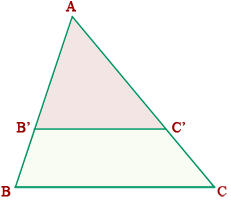
Lo que se traduce en la fórmula

Hagamos un ejercicio como ejemplo:

 En el triángulo de abajo, hallar las medidas de los segmentos a y b .ç

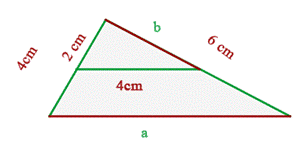
Aplicamos la fórmula, y tenemos

     








Del primer teorema de Tales se deduce además lo siguiente (realmente es otra variante de dicho teorema, y, a su vez, consecuencia del mismo):

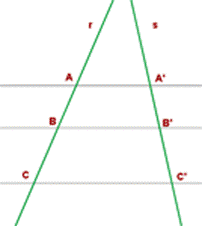
Si dos rectas cualesquieras (r y s) se cortan por varias rectas paralelas (AA’, BB’, CC’) los segmentos determinados en una de las rectas (AB, BC) son proporcionales a los segmentos correspondientes en la otra (A’B’, B’C’).

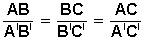
Ejercicios

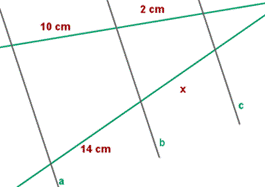
1. Las rectas a, b y c son paralelas. Hallar la longitud de x.

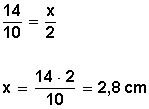
2.Las rectas a, b son paralelas. ¿Podemos afirmar que c es paralela a las rectas a y b?

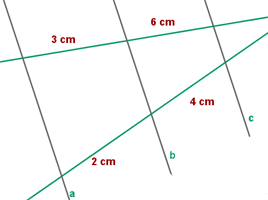Sí , porque se cumple el teorema de Thales .

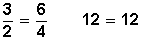Una aplicación inmediata de este teorema sería la división de un segmento en partes iguales, o en partes proporcionales a números dados.