EJEMPLO#7 Calcula el área limitada entre la siguiente función y el eje x:

El área limitada por esta función y el eje x será el área que quede entre la función y los puntos de corte con el eje x, que a su vez serán los límites de integración.

Por tanto, lo primero que tenemos que hacer es calcular los puntos de corte de la función con el eje x.

La función corta con el eje x cuando es igual a cero, por lo que debemos igualar a cero la función y resolver la ecuación de segundo grado que resulta:

Cuyas soluciones son:

Por tanto, la función corta al eje x en los puntos x=-1 y x=2.

Si representamos la función nos queda:

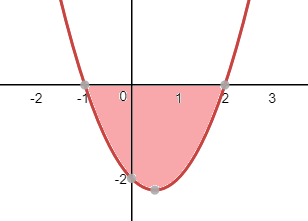
El área que tenemos que calcular queda por debajo del eje x, por lo que será igual a la integral de la función entre -1 y 2, y precedida por un signo menos:

Para eliminar el signo menos, le damos la vuelta a los límites de integración:

Ahora aplicamos la regla de  Barrow.

Integramos la función y la dejamos entre corchetes con sus límites de integración:

Realizamos al resta de las funciones primitivas correspondientes sustituyendo la x por -1 y por 2 respectivamente::

Operamos, dejando el segundo paréntesis, ya que tiene delante un signo menos y no equivocarnos en los signos:

Y ahora sí, eliminamos el segundo paréntesis, cambiando de signo los términos que tiene dentro:

Finalmente, reducimos a común denominador y operamos hasta llegar al resultado final:

El área limitada entre la función y el eje x tiene un valor de 9/2 unidades cuadradas.

EJEMPLO#6

Calcular el área limitada por la curva y = x² -5x + 6 y la recta y = 2x.

En primer lugar hallamos los puntos de corte de las dos funciones para conocer los límites de integración.

De x = 1 a x = 6, la recta queda por encima de la parábola.

EJEMPLO #5

Calcular el área limitada por la curva y = 6x² − 3x³ y el eje de abscisas.

Ejemplo #4

Hallar el área limitada por la recta x + y = 10, el eje OX y las ordenadas de x = 2 y x = 8.

Ejemplo # 3

Hallar el área de la región del plano encerrada por la curva y = ln x entre el punto de corte con el eje X y el punto de abscisa x = e

En primer lugar calculamos el punto de corte con el eje de abscisas.

EJEMPLO #2

Calcular el área del recinto limitado por la curva y = 4x − x² y el eje X. En primer lugar hallamos los puntos de corte con el eje X para representar la curva y conocer los límites de integración.

0 = 4x − x²

^{0=X(4-X)>>>>>>>>>ENTONCES x=0 y x=4}

En segudo lugar se calcula la integral:

Integrales Definidas

Integral definida. Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x = a y x = b.

Definición

La integral definida es uno de los conceptos fundamentales del Análisis Matemático.

La integral definida de f(x) en el intervalo [a,b] es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x = a y x = b (bajo la hipótesis de que la función f es positiva). Esta integral se representa por:

a es límite inferior de la integración y b es límite superior de la integración.

Si la función F es una función primitiva de f en el intervalo [a,b], por la Regla de Barrow se tiene que:

Propiedades

1. El valor de la integral definida cambia de signo si se permutan los límites de integración.

2. Si los límites que integración coinciden, la integral definida vale cero.

3. Si c es un punto interior del intervalo [a, b], la integral definida se descompone como una suma de dos integrales extendidas a los intervalos [a, c] y [c, b].

4. La integral definida de una suma de funciones es igual a la suma de integrales·

5. La integral del producto de una constante por una función es igual a la constante por la integral de la función.

EJEMPLO #1: Integral como Àrea debajo de una curva 

Teoremas de Thales

Cuando en geometría hablemos del Teorema de Tales (o Thales) , debemos aclarar a cuál nos referimos ya que existen dos teoremas atribuidos al matemático griego Tales de Mileto en el siglo VI a. C. Primer teorema Como definición previa al enunciado del teorema, es necesario establecer que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre si. El primer teorema de Tales recoge uno de los postulados más básicos de la geometría, a saber, que:Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes.
Entonces, veamos el primer Teorema de Tales en un triángulo :
Dado un triángulo ABC , si se traza un segmento paralelo, B'C', a uno de los lados del triángulo, se obtiene otro triángulo AB'C' , cuyos lados son proporcionales a los del triángulo ABC .


Lo que se traduce en la fórmula

Hagamos un ejercicio como ejemplo:

 En el triángulo de abajo, hallar las medidas de los segmentos a y b .ç

Aplicamos la fórmula, y tenemos

     








Del primer teorema de Tales se deduce además lo siguiente (realmente es otra variante de dicho teorema, y, a su vez, consecuencia del mismo):

Si dos rectas cualesquieras (r y s) se cortan por varias rectas paralelas (AA’, BB’, CC’) los segmentos determinados en una de las rectas (AB, BC) son proporcionales a los segmentos correspondientes en la otra (A’B’, B’C’).

Ejercicios

1. Las rectas a, b y c son paralelas. Hallar la longitud de x.

2.Las rectas a, b son paralelas. ¿Podemos afirmar que c es paralela a las rectas a y b?

Sí , porque se cumple el teorema de Thales .

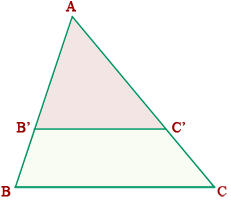
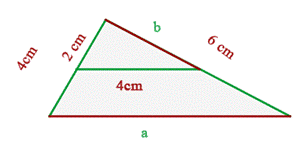
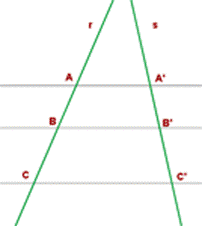
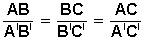
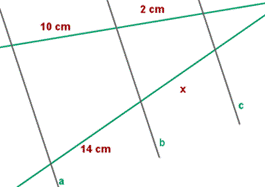
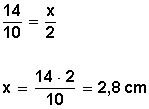
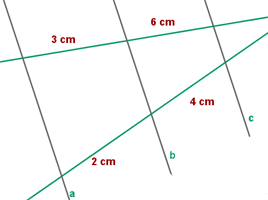
Una aplicación inmediata de este teorema sería la división de un segmento en partes iguales, o en partes proporcionales a números dados.